Attempting to re-write in C++ the Gillespie algorithm, which I earlier implemented in R, I stumbled upon the fact that sampling from various probability distributions is not so straightforward in C++. Luckily, all I needed was the exponential distribution, where the Inverse Cumulative Distribution Function offers an elegant workaround. This post contains the explanantion and implementation of the method.

In general, this method allows to sample from a distribution that is not readily available. To be more precise, given a probability density function $f(x)$ (for continuous variables) or probability mass function $p(x)$ (for discrete variables) or, alternatively, cumulative distribution function $F(x)$ we would like to generate $x$ such that $P(X \le x) =F(x).$ The Inverse Cumulative Distribution Function (ICDF) method, also called the inverse transform method, allows to generate random variables following a distribution with a known explicit form of the ICDF. The simulation is enabled by the generalised inverse function (the quantile function) $F^{-}(u)=min {x: F(x) \ge u}, u \in [0,1]$ with the properties $ F^{-1}(F(x)) \le x$ and $ F(F^{-1}(u)) \le u.$ For continuous random variables this will be a regular inverse CDF. The properties of the ICDF suggest the inverse transform method:
Given a CDF $F,$ if $u$ is distributed uniformly on $(0,1)$, then $x=F^{-1}(u)$ is distributed as $F,$ that is $P(X \le x) =F(x).$
This method makes simulation of variables following such continuous distributions as Exponential, Cauchy, Logistic, truncated Normal and Pareto distributions straightforward. Knowledge of the relationships between distributions provides ways of deriving simulations of, for instance, Chi Squared, Gamma and Beta from the Exponential. In the same way Student’s distribution can be derived from Cauchy.
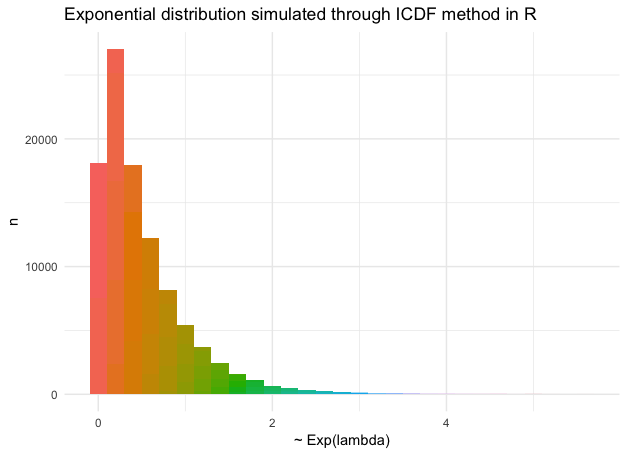
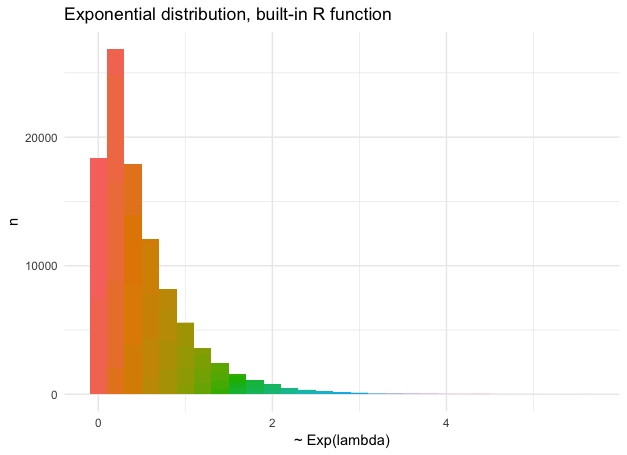
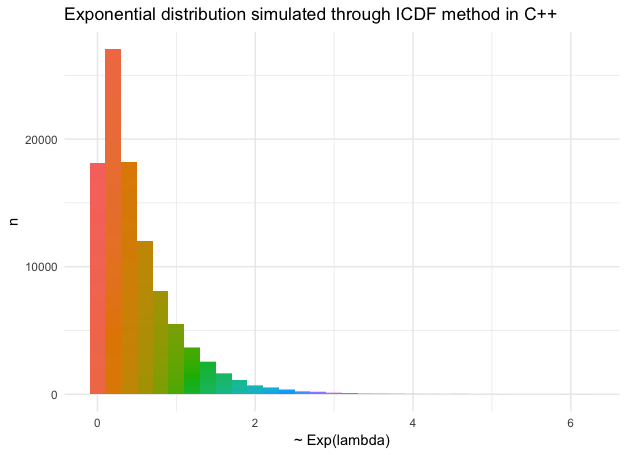
In the codes presented below I implemented the ICDF method to sample from the Exponential distribution with parameter $\lambda$. The plots aim to compare the simulations resulting from the C++ and R implementations based on ICDF, as well the the built-in R functionality.
Similar to the previous post we can use the workflow to compile and execute the C++ code with
sh compileICDF.sh
Which other obstacles are awaiting on the path of translating the Gillespie algorithm into C++? Stay tuned and I will keep you posted!